昨天在看DP算法,特意开篇文章记录下,加深一下印象。本文围绕著名的01背包展开讨论。
开始DP之前
提起DP,就给我一种难到天迹的感觉,实际上DP要是难起来也确实没边,通过学习DP算法也发现自己在逻辑推理以及阅读包含大量公式文章上的效率不足。
在讲我对DP的理解之前,我想回顾下斐波那契数列(Fibonacci sequence),想必大家对这个并不陌生,就像下面这样。
$${1,1,2,3,5,8,13,21····}$$
我们已经知道斐波那契的计算公式为
$$fib(n) =\left.
\begin
\end1 & n=1,2\fib(n-1)+fib(n-2) & n>2\
\right.
$$
如果我们使用递归求fib(5),展开是这个样子的。
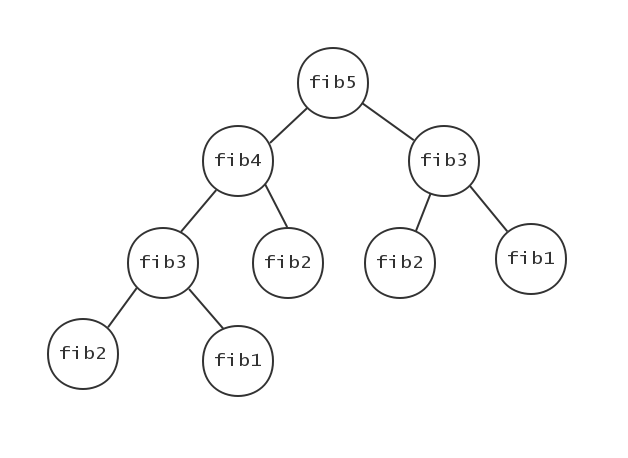
从中不难看出我们在使用递归算法自顶向下求$fib(5)$的时候,求了两次$fib(3)$,三次$fib(2)$,如果n值越大,其中的重复求解就会越多,并且这类求解都是已经求过的,不是新产生的问题(求$fib(7)$的时候不会出现求解$fib(10)$的情况),这类重复的求解的问题,我们称之具有重叠子问题性质
在递归求解中,我们实际上只需要递归到子问题$fib(1)=1,fib(2)=1$即可求解问题,因为$fib(1),fib(2)$值是确定的,所以我们可以理解为只要$fib(1),fib(2)$的值一旦确定,后续的$fib(3),fib(4)···fib(N)$的值也是确定的,我们称之为无后效性,即该阶段状态已知,则后续发展阶段的状态仅跟前一阶段状态有关,而和其他阶段状态无关。
简单讲,动态规划算法适用具有以下性质的问题
重叠子问题:子问题重叠性质是指在用递归算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。wiki
无后效性:无后效性是指如果在某个阶段上过程的状态已知,则从此阶段下一过程的发展变化仅与此阶段的状态有关,而与过程在此阶段以前的阶段所经历过的状态无关。
最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质(即满足最优化原理)。wiki
关于0/1 Knapsack Problem 的思考过程
问题描述
给定$N$个物品,每个物品有一个重量$W$和一个价值$V$.你有一个能装M重量的背包.问怎么装使得所装价值最大.每个物品只有一个.
输入格式
输入的第一行包含两个整数$n$, $m$,分别表示物品的个数和背包能装重量。
以后$N$行每行两个数$Wi$和$Vi$,表示物品的重量和价值
输出格式
输出1行,包含一个整数,表示最大价值。
样例输入
3 5
2 3
3 5
4 7
样例输出
8
数据规模和约定
$1<=N<=200,M<=5000.$
来自 http://lx.lanqiao.cn/problem.page?gpid=T287
首先是状态转移方程
我们特别约定
| 符号 | 含义 |
|---|---|
| $N$ | 物品的件数 |
| $Ni$ | 第 $i$ 件物品 |
| $V$ | 背包的总容量 |
| $v$ | 当前背包的容量 |
| $Ci$ | 第 $i$ 个物品消耗的容量 |
| $Wi$ | 第 $i$ 个物品获取的价值 |
假设我是一个背着容量为20麻袋的小偷,来到了仓库中,那么我遇到了以下选择。
$$ Choice =\left.
\begin
\endCi>v & 不偷 \Ci<v & 偷或者不偷 \
\right.
$$
假设当前的背包容量$v>Ci$,那么我们就需要考虑偷和不偷两种情况。偷和不偷的状态转移方程则就是
$$ Max =\left.
\begin
F[i,v]=F[i-1,v]&不偷\
F[i,v]=F[i-1,v-Ci]
\end+Wi&偷\
\right.
$$
在这里$F(i,v)$,我们表示前i件物品刚好放入空间为$v$的背包中产生的总价值,F(3,10)就代表我前三件物品,占用10空间屎产生的价值,所以不偷的状态转移方程就很好理解了,如果第$i$件物品我选择不拿,那么$F(i,v)$的价值和背包剩余空间没有发生改变,和$F[i-1,v]$一致,也就是拿$i-1$件物品状态。我们只要沿用$F[i-1,v]$状态就可以了。
$$F[i,v]=F[i-1,v]$$
但是如果我拿了呢,那么状态方程中的价值和空间就应该更新。他的总价值基于什么发生改变呢?很明显,我在拿了前$i-1$件物品的基础上,我的价值增加了$Wi$也就是$F[i-1,v]+Wi$,那么此时我的空间发生了什么变化,当然是减去第$i$件商品的重量$Ci$啦,那么我的状态就是$F[i-1,v-Ci]+Wi$的状态,此时我们更新该状态。
$$F[i,v]=F[i-1,v-Ci]+Wi$$
现在回过头来,其实装不下的时候,我们也可以归类为不偷这一状态。那么到这里,状态转移方程我们已经搞清楚了。
$$ Max =\left.
\begin
F[i,v]=F[i-1,v]&装不下,不偷\
F[i,v]=F[i-1,v]&装的下,不偷\
F[i,v]=F[i-1,v-Ci]
\end+Wi&装的下,偷\
\right.
$$
那么我们的决策策略,也就出来了,装不下的之后不偷,装的下的时候我们选偷和不偷两种策略中的最佳策略,这样我们就能保证我们的决策是当前最优,即局部最优,从而得到全局最优解或者说近似最优解。
算法设计和实现
空间复杂度$O(NV)$
由于动态规划的过程中我们需要访问之前的状态,所以我们需要设计个东西存放状态,这里我们采用二维数组的方式。
即$F[N][V]$,也就是$N*V$大小的数组,为了算法实现(物品从1编号)比较方便,我们实际上采用$F[N+1][V+1]$大小的空间,最后$F[N][V]$中存放的就是我们的目标结果。
通过双层for进行遍历,伪代码示意如下
F[N+1][V+1]={0};初始化数组都为0
for i←1 to N //从1号物品到N号物品
for v←Ci to V //背包空间从1-V
if(Ci>v) //第i个物品的重量大于当前背包容量
F[i,v]=F[i-1,v]; //装不下,不拿
else //可以拿的时候,取拿或者不拿的最优解。
F[i,v]=max(F[i-1,v],F[i-1,v-Ci]+Wi);
实际的遍历过程示意 i从小到大,v从小到大
| $v→V$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $Ni$ | $Ci$ | $Wi$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 5 | 0 | 0 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 2 | 3 | 7 | 0 | 0 | 5 | 7 | 7 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| 3 | 6 | 4 | 0 | 0 | 5 | 7 | 7 | 12 | 12 | 12 | 12 | 12 | 12 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| 4 | 3 | 8 | 0 | 0 | 5 | 8 | 8 | 13 | 15 | 15 | 20 | 20 | 20 | 20 | 20 | 20 | 24 | 24 | 24 | 24 | 24 | 24 | 24 |
| 5 | 4 | 5 | 0 | 0 | 5 | 8 | 8 | 13 | 15 | 15 | 20 | 20 | 20 | 20 | 25 | 25 | 25 | 25 | 25 | 25 | 29 | 29 | 29 |
空间复杂度$O(V)$
我们前面提到动态规划算法适用问题中有个特性叫做无后效性,也就是i阶段仅和前一阶段 $i-1$ 的状态有关,放到本问题中就是,我的求解数组,仅仅和前一组数据有关。
回顾前面的算法我们知道,第 $i$ 件物品无论放还是不放的状态转移方程仅和前 $i-1$ 件物品的状态有关,并且前$i-1$件物品总价值存放在第$F[i-1,v]$中。$v$ 则不断递增。
如果我们使用一个一维数组$dp[V+1]$来存放状态,那么我我们就要保证我们能正常访问$F[i-1,v]$和$F[i-1,v-Ci]$,实际上是完全可以的,我们需要略微改动一下状态转移方程。
$$Max=\left.
\begin
dp[v]=dp[v]&装不下,不偷\
dp[v]=dp[v]&装的下,不偷\
dp[v]=dp[v-Ci]
\end+Wi&装的下,偷\
\right.
$$
看到这里,我们再思考一个问题,如果$Ci>v$怎么办?这样数组就越界了。所以我们需要保证$v>Ci$,并且内层for循环需要逆序访问即$V→v$,不然$F[i,v]$值实际上是就变成了$F[i,v-Ci]$而来。这里你追踪下值的变化即可发现。
说白了就是我$v$从小到大开始求的时候,小容量的值更新后就是第$i$轮的了,如果后面需要用 $i-1$ 轮的,就没法用了。
注意 dp数组需要进行初始化操作,最开始背包中并没有物品,所以价值为0。在具体的算法设计中可以预先初始化dp数组,并从物品1开始。
伪代码示意如下
dp[V+1]={0}; //初始化数组都为0
for i←1 to N //从1号物品到N号物品
for v←V to Ci && v>=Ci //背包空间从V到1,v大于等于Ci,反之不可拿,
//这里优化掉了,因为不拿的时候值不用更新,所以只考虑拿的时候值才会更新
dp[v]=max(dp[v],dp[v-C[i]]+W[i]); //可以拿时取最优
实现代码
#include <iostream>
#define MAXN 201
#define MAXM 5001
using namespace std;
int F[MAXN][MAXM]= {{0}};
int main () {
int N,V;
cin>>N>>V;
int dp[V+1]= {0};
int C[N+1]= {0},W[V+1]= {0};//花费C(单个物体的重量),获得价值W
//数据读入
for(int i=1; i<=N; i++) {
cin>>C[i]>>W[i];
}
//空间复杂度O(NV)
int i,v;//第i件物品,当前背包容量v
for(i=1; i<=N; i++) {//第1到第N件物品
for(v=C[i]; v<=V; v++) {//背包空间C[i]到V;
if(C[i]>v) {//能不能放下
F[i][v]=F[i-1][v];//不放
} else {
F[i][v]=max(F[i-1][v],F[i-1][v-C[i]]+W[i]);//取放和不放的最优解
}
}
}
std::cout<<F[N][V]<<endl;
//空间复杂度O(V)
for(i=1; i<=N; i++) {
for(v=V; v>=C[i]; v--) {
dp[v]=max(dp[v],dp[v-C[i]]+W[i]);
}
}
std::cout<<dp[V]<<endl;
//输出二维数组F
cout<<"O(NV)"<<endl;
for(int i=1; i<=N; i++) {
for(int j=1; j<=V; j++) {
cout<<F[i][j]<<" ";
}
cout<<endl;
}
//输出一维数组dp
cout<<"O(N)"<<endl;
for(int i=1; i<=V; i++) {
cout<<dp[i]<<" ";
}
cout<<endl;
return 0;
}